Association de la guerre électronique de l’armée de terre
La radiogoniométrie (1)
1er février 2012.
Cette série de 4 articles est tirée du TRS1360 "Collection des manuels du Sous-Officier spécialiste des Transmissions" datant de 1957. Il s’agit du tome 10 et traite des écoutes et de la radiogoniométrie.
La radiogoniométrie complément des écoutes.
La radiogoniométrie a pour rôle de déterminer, avec le plus de précision possible, la position géographique d’un émetteur. Comme telle, elle permet de compléter et de préciser les résultats donnés par les écoutes en plaçant sur la carte les réseaux et les organismes dont l’analyse a révélé la structure administrative ou les relations de dépendance.
Notons de suite que si les écoutes ne peuvent donner tous les renseignements désirables, c’est-à-dire l’articulation complète de l’organisation ennemie, de même la radiogoniométrie ne peut préciser les emplacements dans tous les cas, le problème étant très complexe. Mais les résultats partiels qu’elle peut donner complètent avantageusement les résultats des écoutes.
1.1 Modes d’utilisation de la radiogoniométrie.
Un radiogoniomètre est un appareil qui utilise les propriétés directives d’un système d’aériens afin de déterminer la direction d’arrivée des ondes provenant d’un émetteur. Cette direction coïncide en général avec la direction vraie de l’émetteur, à une certaine erreur près.
Il faut donc au minimum deux radiogoniomètres pour donner deux relèvements et déterminer la position approchée de l’émetteur. En utilisant un plus grand nombre de radiogoniomètres et un plus grand nombre de relèvements pour chaque appareil, il est possible, comme on le verra par la suite, d’améliorer la précision de la localisation.
La détermination de la position d’un émetteur peut être envisagée de deux manières distinctes :
1.1.1 - Ou bien cette détermination fait partie d’un ensemble organisé : c’est le cas d’un navire, d’un avion demandant son relèvement pour déterminer sa position. Il émet, alors sur des fréquences bien déterminées, sur lesquelles le réseau radiogoniométrique veille en permanence. Les fréquences sont choisies de manière à présenter le moins d’anomalies de propagation possible et une fréquence correspond à une zone de distance de relèvement bien déterminée. Exemples : la fréquence de 333 kHz est employée à moyenne distance par la marine et l’aviation ; la fréquence de 9180 kHz est employée à grande distance par l’aviation ; la fréquence de 120 MHz est employée par les réseaux de navigation aérienne à faible distance (100 à 200 km). Dans ces cas les radiogoniomètres sont réglés pour présenter l’efficacité maximum sur les fréquences de travail.
Ce mode d’utilisation correspond à la "radiogoniométrie de navigation".
1.1.2 - Ou bien un réseau radiogoniométrique travaille à la localisation d’émetteurs quelconques, travaillant sur des fréquences quelconques, parfois avec des émissions de durée très brève, des aériens directionnels, etc.
Le problème devient beaucoup plus complexe ; c’est la "radiogoniométrie d’ interception".
1.2 - Caractéristique de la radiogoniométrie d’interception.
Les radiogoniomètres doivent couvrir une gamme de fréquence très étendue : il est parfois nécessaire de grouper ensemble plusieurs appareils différents. De plus les conditions de propagation varient beaucoup le long de ces gammes : un ou plusieurs radiogoniomètres du réseau peuvent très bien tomber dans la zone de silence d’un émetteur et même si l’émission est perçue par tous les appareils, ce fait peut introduire d’importantes causes d’erreurs. Enfin les appareils doivent être sensibles à des champs très faibles, puisque souvent ils travailleront à limite de portée.
L’implantation même du réseau doit tenir compte de toutes ces conditions, assurer pour toute la zone de travail une parallaxe [1] correcte et prévoir des liaisons entre stations. De plus l’installation elle-même d’un appareil radiogoniométrique pose des conditions assez difficiles à réunir sur le terrain, sans parler des conditions strictement militaires comme celles de la protection, du camouflage, etc...
Matériels de radiogoniométrie
2.0 – Principes des radiogoniomètres.
L’identité de nature des ondes lumineuses et des ondes hertziennes a permis de penser dès le début de l’exploitation de ces dernières qu’il serait possible de faire des visées radioélectriques comme l’on fait des visées optiques, avec l’avantage supplémentaire de pouvoir opérer à des distances bien supérieures, grâce à la grande portée des ondes hertziennes. De cette idée sont nés les radiogoniomètres, appareils permettant de déterminer la direction d’une station émettrice, ou plus exactement la direction d’arrivée des ondes émises par cette station, la propagation ne s’effectuant pas toujours exactement suivant la ligne la plus directe (arc de grand cercle) joignant les stations émettrices et réceptrices.
 Le relèvement radiogoniométrique (le relèvement est la détermination de la direction d’arrivée des ondes) permet de connaître l’azimut, c’est-à-dire l’angle que fait cette direction avec le méridien passant par le radiogoniomètre.
Cet azimut s’exprime généralement en degrés, comptés de 0 à 360 dans le sens des aiguilles d’une montre à partir de la direction du Nord géographique.
Le relèvement radiogoniométrique (le relèvement est la détermination de la direction d’arrivée des ondes) permet de connaître l’azimut, c’est-à-dire l’angle que fait cette direction avec le méridien passant par le radiogoniomètre.
Cet azimut s’exprime généralement en degrés, comptés de 0 à 360 dans le sens des aiguilles d’une montre à partir de la direction du Nord géographique.
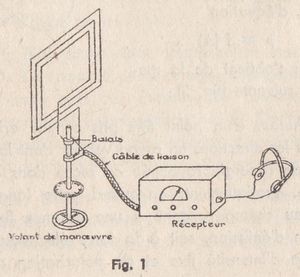
Tout radiogoniomètre se compose essentiellement d’un aérien directif et d’un récepteur alimenté par cet aérien, ainsi que d’un système d’indication de l’azimut (fig. 1).
Le radiogoniomètre le plus simple est ainsi constitué :
a) d’un cadre tournant (aérien directif) dont l’axe de rotation est muni d’un disque gradué permettant de repérer l’azimut ;
b) d’un récepteur normal muni d’un casque ou haut-parleur.
2.0.1 - Diagrammes de directivité d’un aérien.
Un aérien directif est un aérien qui a la propriété de ne pas rayonner ou recevoir l’énergie électromagnétique avec une égale efficacité dans toutes les directions.
 Il est commode de représenter cette propriété au moyen d’une figure, appelée "diagramme de directivité", d’équation
Il est commode de représenter cette propriété au moyen d’une figure, appelée "diagramme de directivité", d’équation
![]() =f (
=f (![]() )
)
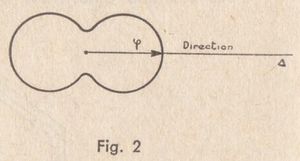
et qui s’obtient de la manière suivante (fig. 2) :
Autour d’un point fixe pris comme origine, on porte dans toutes les directions un rayon vecteur dont la longueur ![]() est fonction de l’énergie rayonnée ou reçue dans la direction
est fonction de l’énergie rayonnée ou reçue dans la direction ![]() considérée. Pratiquement, on prend cette longueur proportionnelle soit au champ rayonné à une distance fixe dans le cas d’un aérien d’émission, soit à la force électromotrice induite par un champ d’intensité fixe et de polarisation donnée dans le cas d’un aérien de réception (d’après le théorème de réciprocité, les deux diagrammes ainsi obtenus sont en général identiques), soit au logarithme de l’une de ces quantités.
considérée. Pratiquement, on prend cette longueur proportionnelle soit au champ rayonné à une distance fixe dans le cas d’un aérien d’émission, soit à la force électromotrice induite par un champ d’intensité fixe et de polarisation donnée dans le cas d’un aérien de réception (d’après le théorème de réciprocité, les deux diagrammes ainsi obtenus sont en général identiques), soit au logarithme de l’une de ces quantités.
Dans la suite du présent texte, les diagrammes tracés seront toujours obtenus en portant des longueurs proportionnelles à l’amplitude de la force électromotrice induite dans l’antenne de réception par un champ d’intensité fixe.
Le lieu géométrique des extrémités des rayons vecteurs considérés est une surface qui est, par définition, le diagramme de directivité. Il est difficile de représenter une telle surface sur une feuille de papier ; d’autre part, ce qui nous intéresse dans le cas de la radiogoniométrie, est de savoir comment sont reçues les ondes électromagnétiques se propageant dans une direction sensiblement horizontale autour du radiogoniomètre.
Nous tracerons donc pour chaque aérien étudié l’intersection de la surface du diagramme de directivité par un plan horizontal passant par l’origine. Cela nous donnera une courbe, appelée "diagramme de directivité horizontale" ou, par abréviation, "diagramme de directivité" (![]() représente alors l’azimut, angle de la direction considérée avec celle du Nord).
représente alors l’azimut, angle de la direction considérée avec celle du Nord).
2.0.2 - Relèvements - Bruit de fond - Plage.
Les diagrammes de directivité qu’on rencontre en général présentent des maximums assez flous et des minimums assez nets : la variation de tension est importante pour un faible écart angulaire de part et d’autre du minimum.
Un type de diagramme assez fréquemment rencontré est le diagramme en "8" composé de deux cercles tangents (figure 10).
Les deux maximums sont peu accusés ; au contraire, les deux minimums correspondent à une grande acuité. On fait donc travailler les radiogoniomètres le plus souvent à l’extinction, ce qui correspond à un minimum très accusé du diagramme de directivité.
Dans de très bonnes conditions de relèvement, l’extinction correspond à un écart angulaire inférieur au demi degré, c’est-à-dire que la direction du relèvement est déterminée à un quart de degré près environ.
Lorsque les conditions sont moins bonnes, il n’y a plus d’extinction nette, mais seulement un minimum : le signal reçu étant faible peut être noyé dans le bruit de fond du récepteur ou les bruits parasites extérieurs. On définit la plage d’un radiogoniomètre, au voisinage de l’angle de relèvement, comme étant l’angle à l’intérieur duquel la variation du signal est trop faible pour être décelée, soit que le signal soit noyé sous le bruit, soit qu’il soit encore audible mais que son intensité soit pratiquement constante.
Les diagrammes de directivité des aériens généralement utilisés possèdent des axes de symétrie : c’est-ci-dire que le relèvement obtenu est affecté d’une incertitude de 180°. Ce fait, généralement sans importance, peut dans certains cas être gênant : il suffit alors de modifier par un procédé quelconque le diagramme de directivité pour faire disparaitre cette symétrie et refaire un relèvement même peu précis qui permettra de "lever le doute" de 180°. On définit le lever de doute comme l’opération permettant de lever cette incertitude ; le dispositif utilisé pour cette opération est souvent désigné par la même expression.
2.0.3 - Rôle du sol.
Il convient de noter dès à présent le rôle primordial joué par le sol en radiogoniométrie. Un sol parfaitement conducteur joue en électricité le rôle d’un miroir et dans le rayonnement de tout aérien, c’est l’antenne elle-même et son image dans ce miroir qui interviennent. Si le sol n’est pas parfaitement conducteur, ses propriétés sont variables, en particulier avec les conditions atmosphériques et les caractéristiques de l’aérien sont, par suite, également variables.
En particulier, la directivité de l’aérien, caractéristique utilisée en radiogoniométrie, varie en même temps que les propriétés du sol. Si le sol est naturellement bon conducteur, ses propriétés restent assez constantes en présence des variations atmosphériques. De bonnes prises de terre suffisent alors pour assurer une directivité constante aux aériens.
Si le sol est mauvais conducteur, on est forcé souvent de le recouvrir d’un réseau métallique de dimensions importantes qui supplée localement à ses mauvaises propriétés. Beaucoup des causes d’anomalies ou de mauvais fonctionnement des radiogoniomètres proviennent des propriétés du sol au voisinage de l’appareil.
2.0.4 - Rappel sur la forme des ondes électromagnétiques.
2.0.4.1 - Champ électromagnétique.
Une antenne d’émission produit dans l’espace qui l’entoure un champ électromagnétique ; c’est-à-dire qu’en tout point de cet espace des charges électriques ou des masses magnétiques se trouvent soumises à des forces qui tendent à les faire mouvoir.
Ces champs peuvent se représenter commodément par des flèches (vecteurs) dont la direction, le sens et la longueur représentent la direction, le sens et la grandeur de la force correspondante, lorsque la charge électrique ou la masse magnétique soumise au champ a une valeur égale à l’unité choisie. Dans la suite, nous ne considérerons plus que le champ électrique, étant entendu que les deux champs électrique et magnétique coexistent toujours.
Le champ se propage autour de l’antenne d’émission. Le lieu géométrique des points atteints au même instant par le champ qui a été émis par l’antenne émettrice à un autre instant choisi comme origine des temps est par définition une "surface d’onde".
2.0.4.2 - Plans d’onde.
Si l’on se trouve à une distance assez grande de l’antenne émettrice, on peut avec une très bonne approximation confondre la surface d’onde avec son plan tangent au point ou l’on se trouve.
Ce plan prend le nom de plan d’onde. Ses propriétés sont les suivantes :
en tout point d’un même plan d’onde et à un instant donné, le champ a même grandeur, direction et sens. Le plan d’onde est perpendiculaire à la direction de propagation.
On peut décomposer le champ électrique existant à un moment donné et dans un plan d’onde donné en trois composantes perpendiculaires entre elles. L’une des composantes ![]() , sera choisie verticale,
, sera choisie verticale,
 les deux autres horizontales l’une
les deux autres horizontales l’une ![]() dirigée suivant la trace du plan d’onde sur le plan horizontal, l’autre
dirigée suivant la trace du plan d’onde sur le plan horizontal, l’autre ![]() dirigée suivant la projection horizontale de la direction de propagation (fig. 3).
dirigée suivant la projection horizontale de la direction de propagation (fig. 3).
En un même point de l’espace ces trois composantes varient au cours du temps suivant une loi sinusoïdale, et l’on peut écrire :
![]()
![]() (1)
(1)
![]()
![]() ,
, ![]() ,
, ![]() sont par définition les amplitudes des trois composantes du champ ;
sont par définition les amplitudes des trois composantes du champ ; ![]() ,
, ![]() et
et ![]() sont les phases de ces mêmes composantes, et dépendent du choix de l’origine du temps ;
sont les phases de ces mêmes composantes, et dépendent du choix de l’origine du temps ; ![]() est la pulsation de l’onde ; t est le temps.
Les formules (1) ci-dessus supposent que l’onde est une onde sinusoïdale pure, sans modulation. Une modulation de l’onde ajouterait de nouveaux champs, de pulsations différentes (
est la pulsation de l’onde ; t est le temps.
Les formules (1) ci-dessus supposent que l’onde est une onde sinusoïdale pure, sans modulation. Une modulation de l’onde ajouterait de nouveaux champs, de pulsations différentes (![]() et
et ![]() par exemple s’il s’agit d’une modulation en amplitude avec la pulsation sinusoïdale
par exemple s’il s’agit d’une modulation en amplitude avec la pulsation sinusoïdale ![]() ).
Mais nous ne considérerons pas ces champs supplémentaires dus à la modulation, qui n’apportent aucun changement à l’exposé du fonctionnement des radiogoniomètres. La mesure de l’azimut est d’ailleurs effectuée le plus souvent sur l’onde porteuse seule.
).
Mais nous ne considérerons pas ces champs supplémentaires dus à la modulation, qui n’apportent aucun changement à l’exposé du fonctionnement des radiogoniomètres. La mesure de l’azimut est d’ailleurs effectuée le plus souvent sur l’onde porteuse seule.
Le lieu géométrique de l’extrémité du vecteur champ ![]() est dans le cas le plus général une ellipse de centre O, dont la forme et la position dépendent des amplitudes et des phases relatives des trois composantes. On dit dans ce cas que la polarisation est elliptique.
est dans le cas le plus général une ellipse de centre O, dont la forme et la position dépendent des amplitudes et des phases relatives des trois composantes. On dit dans ce cas que la polarisation est elliptique.
Dans certains cas, cette ellipse se réduit à une droite, le petit axe devenant nul. Les phases ![]() ,
, ![]() et
et ![]() sont alors égales. On dit alors que l’onde a une polarisation rectiligne.
sont alors égales. On dit alors que l’onde a une polarisation rectiligne.
Les axes de l’ellipse peuvent devenir égaux, la polarisation est alors dite circulaire.
A un instant donné, dans une portion d’espace pas trop étendue, tous les plans d’onde sont parallèles. Si l’on passe d’un plan d’onde O à un autre plan d’onde A, la phase des différentes composantes du champ varie linéairement et l’on a :
![]() radians
radians
![]() radians (2)
radians (2)
![]() radians
radians
![]() ,
, ![]() et
et ![]() sont les phases, comptées en radians, des trois composantes du champ
sont les phases, comptées en radians, des trois composantes du champ ![]() existant dans le plan d’onde A ;
existant dans le plan d’onde A ; ![]() ,
, ![]() et
et ![]() celles du champ
celles du champ ![]() existant dans le plan d’onde O.
existant dans le plan d’onde O.
D est la distance normale des deux plans d’onde O et A (fig. 4).
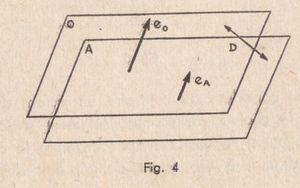 Le segment orienté D = O A se compte positivement dans le sens de la propagation, négativement en sens inverse.
Le segment orienté D = O A se compte positivement dans le sens de la propagation, négativement en sens inverse.
![]() est la longueur d’onde, mesurée avec la même unité que D.
C’est la distance de deux plans d’onde consécutifs dont les phases diffèrent de 2
est la longueur d’onde, mesurée avec la même unité que D.
C’est la distance de deux plans d’onde consécutifs dont les phases diffèrent de 2 ![]() radians, c’est-a-dire dans lesquels on retrouve le même champ en grandeur, direction et sens.
radians, c’est-a-dire dans lesquels on retrouve le même champ en grandeur, direction et sens.
Si l’on reporte les valeurs données par (2) dans les formules (1) on trouve les formules donnant les composantes du champ en tout point d’un plan A situé à la distance D du plan O :
![]()
![]() (3)
(3)
![]()
Ces formules montrent la double périodicité du champ dans le temps et dans l’espace. En effet, si on considère un point fixe de l’espace, D est invariable et le champ varie sinusoïdalement avec le temps.
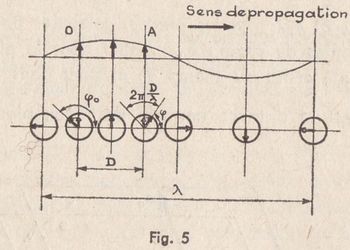 Si l’on considère au contraire un instant donné, t est invariable et le champ varie sinusoïdalement avec D. La figure 5 montre comment se comporte par exemple la composante verticale du champ, à un instant donné, aux différents points de l’espace. Le plan de figure est le plan vertical contenant la direction de propagation. Les traces des différents plans d’onde sur le plan de figure sont des droites verticales. Le vecteur champ vertical peut, d’après les formules (3), être considéré comme la projection verticale d’un vecteur d’amplitude constante
Si l’on considère au contraire un instant donné, t est invariable et le champ varie sinusoïdalement avec D. La figure 5 montre comment se comporte par exemple la composante verticale du champ, à un instant donné, aux différents points de l’espace. Le plan de figure est le plan vertical contenant la direction de propagation. Les traces des différents plans d’onde sur le plan de figure sont des droites verticales. Le vecteur champ vertical peut, d’après les formules (3), être considéré comme la projection verticale d’un vecteur d’amplitude constante ![]() , décalé dans les différents plans d’onde d’un angle égal à
, décalé dans les différents plans d’onde d’un angle égal à ![]() .
.
La position de ces vecteurs décalés est indiquée à la partie inférieure de la figure, pour différents plans d’onde.
Le lieu géométrique de l’extrémité du vecteur champ vertical est donc une sinusoïde. Au cours du temps, cette sinusoïde se déplace dans le sens de propagation. Tous les vecteurs décalés correspondant aux différents points de l’espace tournent avec une vitesse de rotation constante, en conservant entre eux un déphasage constant.
On pourrait répéter pour les composantes horizontales du champ ce qui vient d’être dit pour la composante verticale.
2.0.4.3 - Action du champ électrique sur un conducteur.
Un conducteur renferme toujours un grand nombre de charges électriques libres. A l’état d’équilibre et en l’absence de tout champ, on dit que le corps est neutre au point de vue électrique, c’est-à-dire que la somme des charges positives est égale à la somme des charges négatives. Aucun phénomène électrique ne se manifeste.
En présence d’un champ électrique, les charges sont soumises à des forces qui tendent à les déplacer, et par conséquent à créer un courant électrique. On dit qu’il y a production d’une force électromotrice (en abrégé f.é.m.).
Nous n’aurons pratiquement a considérer que des conducteurs filiformes, c’est-a-dire dont deux dimensions sont très petites par rapport a la troisième.
Dans un tel conducteur l’efficacité du champ et par conséquent la f.é.m. produite, dépend de l’angle que fait la direction du champ avec le fil : si l’on considère un petit élément de conducteur (fig. 6), de longueur ![]() , faisant un angle
, faisant un angle ![]() avec la direction du champ qui, à un instant donné, a une intensité
avec la direction du champ qui, à un instant donné, a une intensité ![]() , la f.é.m. élémentaire produite dans cet élément, à cet instant a pour valeur :
, la f.é.m. élémentaire produite dans cet élément, à cet instant a pour valeur :
![]() (4)
(4)
![]() s’exprime en volts
s’exprime en volts
![]() s’exprime en volts par mètre
s’exprime en volts par mètre
![]() s’exprime en mètres.
s’exprime en mètres.
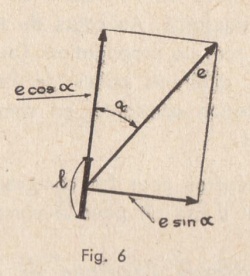 En effet, le champ est une force agissant sur les charges électriques. Comme toute force, il peut être décomposé en deux composantes ; l’une parallèle au fil, de grandeur
En effet, le champ est une force agissant sur les charges électriques. Comme toute force, il peut être décomposé en deux composantes ; l’une parallèle au fil, de grandeur ![]() qui tend à déplacer les charges le long du conducteur, l’autre perpendiculaire au fil, qui a une action nulle, car les charges ne peuvent sortir du conducteur. La f.é.m. est donc maximum lorsque le champ est parallèle au conducteur, et nulle lorsqu’il lui est perpendiculaire.
qui tend à déplacer les charges le long du conducteur, l’autre perpendiculaire au fil, qui a une action nulle, car les charges ne peuvent sortir du conducteur. La f.é.m. est donc maximum lorsque le champ est parallèle au conducteur, et nulle lorsqu’il lui est perpendiculaire.
 II est intéressant de remarquer que l’action d’un champ de direction quelconque sur un élément de conducteur P M Q de longueur
II est intéressant de remarquer que l’action d’un champ de direction quelconque sur un élément de conducteur P M Q de longueur ![]() , de direction également quelconque, peut-être considérée comme équivalente à la somme des actions exercées par ce même champ sur des conducteurs formant un petit circuit ouvert P N Q ayant les mêmes extrémités que l’élément considéré. On peut donc en particulier considérer un conducteur ayant une direction quelconque comme l’équivalent de deux conducteurs en série qui sont les projections verticales et horizontale de ce conducteur. La composante verticale du champ a une action uniquement sur le conducteur vertical équivalent, et la composante horizontale n’a d’action que sur le conducteur horizontal.
, de direction également quelconque, peut-être considérée comme équivalente à la somme des actions exercées par ce même champ sur des conducteurs formant un petit circuit ouvert P N Q ayant les mêmes extrémités que l’élément considéré. On peut donc en particulier considérer un conducteur ayant une direction quelconque comme l’équivalent de deux conducteurs en série qui sont les projections verticales et horizontale de ce conducteur. La composante verticale du champ a une action uniquement sur le conducteur vertical équivalent, et la composante horizontale n’a d’action que sur le conducteur horizontal.
2.0.4.4 - Action de plusieurs champs de même fréquence agissant simultanément sur un conducteur.
On peut appliquer le principe de superposition : la f.é.m. totale produite par l’action simultanée de plusieurs champs est égale à la somme algébrique des f.é.m. produites par chaque champ pris isolément.
Or, on a vu précédemment que le champ dans l’espace pouvait être décomposé en trois champs perpendiculaires entre eux. On peut donc connaitre l’action du champ réel en ajoutant les actions de ces trois composantes. Celles-ci ont la même pulsation ![]() puisqu’elles proviennent du même émetteur. Mais généralement leurs phases ne sont pas égales. Si la portion de
conducteur
puisqu’elles proviennent du même émetteur. Mais généralement leurs phases ne sont pas égales. Si la portion de
conducteur ![]() fait les angles
fait les angles ![]() ,
, ![]() et
et ![]() avec les trois directions de ev, err et ep on a comme valeur de la f.é.m. totale à l’instant t :
avec les trois directions de ev, err et ep on a comme valeur de la f.é.m. totale à l’instant t :
![]() (5)
(5)
Si l’on se donne dans un plan 2 axes perpendiculaires entre eux, Ox et Oy, on peut considérer la f.é.m. totale, à un instant donné, comme la projection sur l’axe Oy de la somme de 3 vecteurs de longueurs respectivement égales à :
![]() Â ;
 ;![]() ;
; ![]()
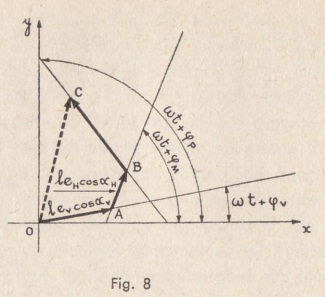 et faisant avec l’axe Ox les angles :
et faisant avec l’axe Ox les angles :
![]() ;
; ![]() ;
; ![]()
Les angles que font entre eux ces 3 vecteurs sont constants au cours du temps, puisqu’ils sont égaux à :
![]()
![]() (6)
(6)
![]()
Ils tournent ensemble avec la vitesse angulaire ![]() . La f.é.m. résultante est donc une fonction sinusoïdale du temps, la figure O A B C restant indéformable en tournant (fig. 8).
. La f.é.m. résultante est donc une fonction sinusoïdale du temps, la figure O A B C restant indéformable en tournant (fig. 8).
2.1 - ETUDE DES TYPES D’AERIENS.
Le diagramme de directivité d’un aérien radiogoniométrique et par conséquent le relèvement donné par le radiogoniomètre dépend de la polarisation de l’onde reçue : l’appareil n’est susceptible de fournir une indication précise que si l’on connait d’une part la direction de la polarisation et de l’autre, une courbe de correction en fonction de la polarisation considérée.
D’une façon générale, cette courbe n’est connue que pour un seul type de polarisation (par exemple polarisation verticale).
On suppose donc que l’onde reçue est entièrement polarisée selon cette direction ou bien que la réponse du système d’antenne aux ondes qui seraient polarisées différemment est de valeur suffisamment faible pour être négligée.
L’inobservation de ces principes restrictifs peut conduire à des erreurs de relèvement connues sous le nom "d’erreurs de polarisation". Le problème des erreurs de polarisation est fondamental en radiogoniométrie. C’est pourquoi, il sera étudié dans le cas de chaque type d’aérien. Pratiquement, on rencontre à peu près uniquement des systèmes d’aériens dérivés du cadre ou de l’antenne verticale.
Dans le cas des cadres ou des dipôles orientables de modèle courant, ces aériens ne peuvent, en raison même de leur nature, donner aucune indication quant à la direction selon laquelle se propage une onde ayant la forme la plus générale, qui est celle de la polarisation elliptique. Ils sont par contre susceptibles d’indiquer celle de certaines composantes du champ. Il peut donc s’y produire des erreurs qui dépendent de la polarisation de l’onde.
Les autres appareils dérivant du type Adcock, comparent les valeurs que prend le champ électromagnétique de l’onde en plusieurs points de l’espace et déterminent ainsi la direction de cette onde. Dans l’appareil le plus simple, deux aériens verticaux identiques sont connectés en opposition à l’entrée du récepteur : l’extinction correspond a l’état d’équiphase qui donne la direction du front de l’onde.
Le relèvement obtenu est exempt d’erreur de polarisation si les réponses respectives des deux aériens verticaux aux ondes reçues sont identiques, quelle que soit la polarisation de ces ondes. De plus, tous les autres éléments du radiogoniomètre doivent être insensibles à la réception directe de l’onde, car toute réception de cette nature donne un diagramme de directivité variable en fonction de la polarisation de l’onde et différent du diagramme de directivité des deux aériens.
Ces différents points seront repris en détail lors de l’étude de chaque aérien.
2.1.1 - Aérien à cadre.
Un cadre est constitué par une ou plusieurs spires de fil conducteur enroulées très sensiblement dans un même plan, et dont les extrémités sont reliées à l’entrée d’un récepteur.
Le cadre est mobile autour d’un axe vertical situé dans son plan et sa rotation est repérée au moyen d’un rapporteur et d’un index.
2.1.1.1 - Fonctionnement du cadre dans le cas de plans d’onde verticaux, avec polarisation verticale.
Nous étudierons tout d’abord le fonctionnement du cadre dans ce cas particulier ; comme nous le verrons par la suite, c’est en effet avec de tels plans d’onde que le cadre a été employé la première fois comme aérien de radiogoniomètre. Dans les autres cas, le cadre peut donner des erreurs importantes.
Considérons d’abord un cadre rectangulaire a une seule spire, dont deux côtés sont verticaux. Le champ à polarisation verticale n’agit que sur les côtés verticaux du cadre, puisqu’il reste perpendiculaire à ses côtés horizontaux (fig. 9).
Considérons les 3 plans d’onde A, B et O passant respectivement par les deux côtés verticaux et par l’axe de symétrie du cadre.
 D’après la formule (4) on a, en faisant la somme des f.é.m. produites dans les côtés verticaux du cadre :
D’après la formule (4) on a, en faisant la somme des f.é.m. produites dans les côtés verticaux du cadre :
![]() (7)
(7)
![]()
(s étant la longueur des côtés verticaux)
car le champ est constant dans un même plan d’onde à un instant donné, et ![]() puisque les côtés verticaux sont parallèles au vecteur champ.
puisque les côtés verticaux sont parallèles au vecteur champ.
En portant dans (7) la valeur de ![]() et
et ![]() donnée par les formules (3) on trouve :
donnée par les formules (3) on trouve :
![]() (8)
(8)
![]()
Car la distance D doit être affectée de signes contraires suivant que l’on va de O vers A ou de O vers B. Si l’on a choisi un sens de rotation déterminé le long du cadre pour compter les forces électromotrices, les deux côtés du cadre se comportent comme deux générateurs mis en opposition et la f.é.m. résultante est égale à la différence des f.é.m. données par les formules (8). On a donc, aux bornes du cadre :
![]() (9)
(9)
Les formules classiques de la trigonométrie nous permettent de transformer cette expression et l’on trouve :
![]() (10)
(10)
Mais ![]() , si d désigne la demi-longueur des côtés
horizontaux du cadre, et
, si d désigne la demi-longueur des côtés
horizontaux du cadre, et ![]() l’angle que fait le plan du cadre avec les plans d’onde.
l’angle que fait le plan du cadre avec les plans d’onde.
Donc :
![]() (11)
(11)
On voit d’après cette formule que la f.é.m. résultante est une f.é.m. sinusoïdale de pulsation ![]() , en quadrature avec le champ existant dans le plan d’onde passant par l’axe du cadre, puisque celui-ci est proportionnel à
, en quadrature avec le champ existant dans le plan d’onde passant par l’axe du cadre, puisque celui-ci est proportionnel à ![]() et que l’on a la relation :
et que l’on a la relation :
![]() (12)
(12)
Enfin l’amplitude de cette f.é.m. est égale à la valeur absolue de :
![]() (13)
(13)
Elle dépend de ![]() et s’annule en même temps que cette quantité, c’est-a-dire pour
et s’annule en même temps que cette quantité, c’est-a-dire pour ![]() radians, K étant un nombre entier quelconque positif ou négatif. On dit alors qu’il y a extinction et la direction de propagation est connue, puisqu’elle se trouve être perpendiculaire au plan du cadre, mais il subsiste une incertitude sur son sens, car l’extinction se retrouve pour une rotation du cadre de
radians, K étant un nombre entier quelconque positif ou négatif. On dit alors qu’il y a extinction et la direction de propagation est connue, puisqu’elle se trouve être perpendiculaire au plan du cadre, mais il subsiste une incertitude sur son sens, car l’extinction se retrouve pour une rotation du cadre de ![]() radians ou 180 degrés, soit un demi-tour.
radians ou 180 degrés, soit un demi-tour.
Pour tracer le diagramme de directivité horizontal du cadre, quand le champ est polarisé verticalement, nous supposons que la longueur des côtés horizontaux est petite devant la longueur d’onde, ce qui est réalisé pratiquement dans la majorité des cas.
Dans ce cas ![]() reste petit, car
reste petit, car ![]() ne peut dépasser 1 en valeur absolue et on peut confondre le sinus avec l’arc correspondant exprimé en radians.
ne peut dépasser 1 en valeur absolue et on peut confondre le sinus avec l’arc correspondant exprimé en radians.
La formule (13) devient :
![]() (14)
(14)
L’amplitude E de la f.é.m. recueillie aux bornes du cadre est alors directement proportionnelle à ![]() .
.
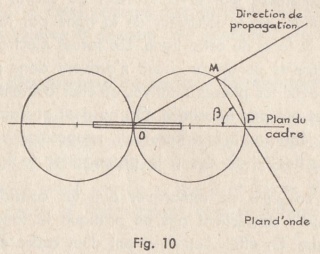 Le diagramme de directivité se compose de deux cercles tangents, et est appelé diagramme en 8. La ligne des centres est dans le plan du cadre. En effet, on voit que l’on a :
Le diagramme de directivité se compose de deux cercles tangents, et est appelé diagramme en 8. La ligne des centres est dans le plan du cadre. En effet, on voit que l’on a :
![]()
MP représentant la trace horizontale d’un plan d’onde et OM la direction de propagation des ondes (fig. 10).
Donc le rayon vecteur OM est proportionnel à ![]() .
.
On voit que l’on pourrait également rechercher la direction de propagation en plaçant le cadre au maximum de réception. Mais en pratique on ne le fait jamais, car la variation de l’intensité de la réception autour du maximum est beaucoup moins rapide, lorsqu’on fait tourner le cadre, qu’elle ne l’est autour du minimum, ainsi qu’on le voit par un simple examen de la figure 10. La précision serait donc beaucoup moins bonne en employant le maximum.
Dans le cas où le cadre comporte plusieurs spires, il est évident que les forces électromotrices produites dans les différentes spires s’ajoutent, et le second membre de la formule (13) est à multiplier par le nombre de spires. Cela n’est d’ailleurs vrai qu’avec une certaine approximation qui devient rapidement trop grossière si la longueur du fil constituant l’enroulement du cadre n’est pas négligeable devant la longueur d’onde. En effet, si une force électromotrice est produite en un point, il lui faut un certain temps pour faire sentir son effet aux extrémités de la ligne constituée par le conducteur du cadre. Ce temps est égal au quotient de la longueur de la ligne par la vitesse de propagation le long de cette ligne. Les forces électromotrices produites en différents points du circuit n’arrivent donc pas aux bornes du cadre avec les phases relatives qu’elles avaient au moment même ou elles ont pris naissance. On ne peut en faire une simple addition algébrique. il faut faire leur composition vectorielle en tenant compte des délais dus à la propagation le long du fil.
Il convient de remarquer que les considérations théoriques ci-dessus n’empêchent pas en pratique le fonctionnement correct du cadre. En effet, l’enroulement d’un cadre est toujours symétrique par rapport à son point milieu, et à tout point situé d’un côté du cadre, on peut faire correspondre un point symétrique. Si des forces électromotrices prennent naissance simultanément en ces deux points, elles mettent le même temps pour atteindre les extrémités opposées de l’enroulement, et rien n’est changé à l’explication du fonctionnement du cadre donnée ci-dessus.
 On peut voir d’ailleurs, grâce à la représentation vectorielle des courants alternatifs, comment fonctionne le cadre au voisinage de l’extinction. Au moment où celle-ci se produit, les deux f.é.m. induites dans les deux côtés verticaux du cadre sont exactement en opposition, les deux vecteurs représentatifs sont égaux et déphasés de 180°, car ces côtés se trouvent dans le même plan d’onde.
Si l’on fait tourner le cadre autour de son axe de symétrie vertical, on fait avancer la phase dans un des côtés, et reculer dans l’autre ; les deux vecteurs représentatifs des f.é.m. se déplacent en sens inverse et donnent une résultante non nulle (fig. 11).
On peut voir d’ailleurs, grâce à la représentation vectorielle des courants alternatifs, comment fonctionne le cadre au voisinage de l’extinction. Au moment où celle-ci se produit, les deux f.é.m. induites dans les deux côtés verticaux du cadre sont exactement en opposition, les deux vecteurs représentatifs sont égaux et déphasés de 180°, car ces côtés se trouvent dans le même plan d’onde.
Si l’on fait tourner le cadre autour de son axe de symétrie vertical, on fait avancer la phase dans un des côtés, et reculer dans l’autre ; les deux vecteurs représentatifs des f.é.m. se déplacent en sens inverse et donnent une résultante non nulle (fig. 11).
2.1.1.2 - Effet d’antenne d’un cadre – Compensation.
Considérons un cadre relié à l’entrée d’un récepteur par des connexions d’une longueur non négligeable par rapport à la longueur d’onde. La composante du champ électrique parallèle à leur direction y induit une f.é.m. qui a la même phase dans les deux conducteurs, si l’on suppose ceux-ci suffisamment rapprochés (fig. 12).
II existe toujours une certaine impédance Z entre le point milieu de l’enroulement du cadre et la terre, soit que ce point milieu y soit directement réuni, soit que cette impédance soit constituée par la capacité répartie de l’enroulement du cadre par rapport à la masse.
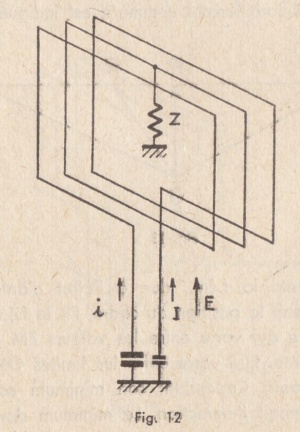 Il en résulte que des courants I et i circulent dans chacune des deux connexions reliant le cadre au récepteur.
Si ces deux connexions, soumises à la même force électromotrice, ne présentent pas des impédances identiques par rapport à la masse, par exemple des capacités inégales, les courants I et i sont inégaux.
Il en résulte que des courants I et i circulent dans chacune des deux connexions reliant le cadre au récepteur.
Si ces deux connexions, soumises à la même force électromotrice, ne présentent pas des impédances identiques par rapport à la masse, par exemple des capacités inégales, les courants I et i sont inégaux.
Les flux magnétiques de sens contraires créés par ces courants circulant dans les deux moitiés du cadre ne s’annulent donc pas exactement. Il subsiste un certain flux magnétique alternatif qui induit dans le cadre une f.é.m. venant s’ajouter à la f.é.m. utile. Elle est en quadrature avec la f.é.m. utile. En effet, les courants I et i, donc les flux magnétiques correspondants, sont en quadrature avec les f.é.m. qui leur ont donné naissance, donc avec le champ, car la réactance des circuits est en général très grande devant leur résistance. Mais d’après les lois de l’induction, les f.é.m. induites sont en quadrature avec le flux magnétique. Elles sont donc en phase ou en opposition avec le champ.
Or nous avons vu que la f.é.m. utile d’un cadre était en quadrature avec le champ existant le long de l’axe de symétrie du cadre. Donc la f.é.m. utile et la f.é.m. due à l’effet d’antenne se composant vectoriellement comme il est indiqué figure 13.
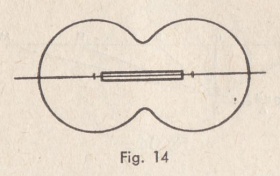
 OP représente la f.é.m. due à l’effet d’antenne qui reste fixe quelle que soit la position du cadre, PR la f.é.m. due à l’effet normal du cadre qui varie entre les valeurs PM et PM’, OR est la f.é.m. résultante. Elle varie entre les limites OM et OM’ mais ne s’annule jamais. Cependant son minimum correspond à la position qui donnait l’extinction. Le minimum devient flou, mais la direction indiquée par ce minimum reste exacte. Le diagramme devient celui de la figure 14.
OP représente la f.é.m. due à l’effet d’antenne qui reste fixe quelle que soit la position du cadre, PR la f.é.m. due à l’effet normal du cadre qui varie entre les valeurs PM et PM’, OR est la f.é.m. résultante. Elle varie entre les limites OM et OM’ mais ne s’annule jamais. Cependant son minimum correspond à la position qui donnait l’extinction. Le minimum devient flou, mais la direction indiquée par ce minimum reste exacte. Le diagramme devient celui de la figure 14.
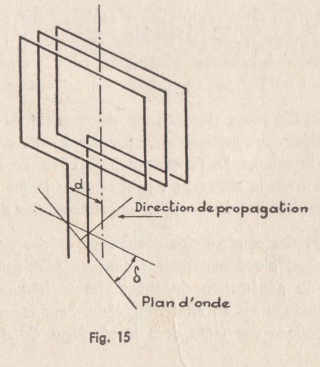
 Si, par suite d’une dissymétrie de construction mécanique, les connexions donnant lieu a la f.é.m. indésirable se trouvent disposées en dehors de l’axe de symétrie du cadre, il s’introduit une phase supplémentaire de cette f.é.m. égale à
Si, par suite d’une dissymétrie de construction mécanique, les connexions donnant lieu a la f.é.m. indésirable se trouvent disposées en dehors de l’axe de symétrie du cadre, il s’introduit une phase supplémentaire de cette f.é.m. égale à ![]() .
.
h étant la distance séparant les connexions de l’axe de symétrie du cadre et ![]() l’angle que fait le plan d’onde avec le plan déterminé par l’axe de symétrie et les connexions du cadre (fig. 15).
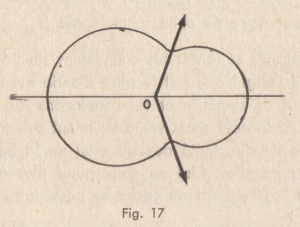
Les f.é.m. se composent alors vectoriellement suivant la fig. 16, et le diagramme de directivité devient celui de la fig. 17, les f.é.m. maxima étant inégales. Om ne correspond plus à la position P
qui donnerait l’extinction si le cadre ne possédait pas l’effet d’antenne.
l’angle que fait le plan d’onde avec le plan déterminé par l’axe de symétrie et les connexions du cadre (fig. 15).
Les f.é.m. se composent alors vectoriellement suivant la fig. 16, et le diagramme de directivité devient celui de la fig. 17, les f.é.m. maxima étant inégales. Om ne correspond plus à la position P
qui donnerait l’extinction si le cadre ne possédait pas l’effet d’antenne.
 Non seulement le minimum est flou, mais sa position est erronnée. D’ailleurs les minima ne sont plus à 180° l’un de l’autre.
Non seulement le minimum est flou, mais sa position est erronnée. D’ailleurs les minima ne sont plus à 180° l’un de l’autre.
 On corrige l’effet dantenne en rendant le cadre et ses connexions aussi symétriques que possibles ; pour cela un ou plusieurs des moyens suivants sont employés :
On corrige l’effet dantenne en rendant le cadre et ses connexions aussi symétriques que possibles ; pour cela un ou plusieurs des moyens suivants sont employés :
- On rend l’entrée du récepteur aussi symétrique que possible, grâce à une construction soignée, à l’emploi d’un transformateur à primaire symétrique, ou à un premier étage symétrique constitué par deux tubes en opposition.
- On place suivant l’axe de symétrie du cadre une antenne supplémentaire verticale. La f.é.m. dans cette antenne est en phase avec le champ. En l’opposant à la f.é.m. parasite, elle même en phase avec le champ, on peut annuler l’effet nuisible en réglant convenablement les amplitudes relatives des deux f.é.m.
- On emploie des connexions et des cadres blindés. Si le cadre est placé entièrement dans un blindage, il ne reçoit plus rien ; la pénétration du champ haute fréquence dans le métal du blindage est en effet très faible. Pour recevoir avec le cadre, on pratique une fente dans le blindage. Ce dernier se comporte lui-même comme un cadre à une seule spire, mais fermé sur un condensateur représenté par les 2 bords de la fente.
 Entre ces 2 bords, les lignes de niveau du champ électrique sont très resserrées et produisent une f.é.m. dans la portion de l’enroulement du cadre placée en ce point. Le blindage étant symétrique par rapport aux deux moitiés de l’enroulement du cadre, l’effet d’antenne est très atténué (fig. 18).
Entre ces 2 bords, les lignes de niveau du champ électrique sont très resserrées et produisent une f.é.m. dans la portion de l’enroulement du cadre placée en ce point. Le blindage étant symétrique par rapport aux deux moitiés de l’enroulement du cadre, l’effet d’antenne est très atténué (fig. 18). - On compense les petites différences qui peuvent subsister dans les réactances des deux connexions au moyen d’un "compensateur" constitué par un petit condensateur à 3 armatures. Deux armatures fixes sont reliées respectivement aux deux extrémités de l’enroulement du cadre, la troisième, mobile, est reliée à la masse.
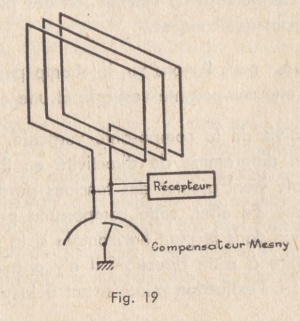 L’armature mobile est telle que pour un sens de rotation donné, sa capacité avec l’une des armatures fixes décroit tandis que sa capacité par rapport à l’autre croit (fig. 19).
L’armature mobile est telle que pour un sens de rotation donné, sa capacité avec l’une des armatures fixes décroit tandis que sa capacité par rapport à l’autre croit (fig. 19).
De cette manière, on arrive à compenser exactement les petites différences de capacité qui peuvent exister dans les connexions du cadre.
On opère pratiquement par approximations successives. Après avoir trouvé un minimum flou, on retouche le compensateur pour rendre ce minimum plus net. On tourne le cadre pour arriver à un minimum plus petit. On recommence à retoucher le compensateur, et ainsi de suite.
